Coronavirus: R-Wert sinkt mit Lockerungen auf unter 1
Der R-Wert des Coronavirus sinkt auf unter 1. Die noch bessere Nachricht: Dabei sind die ersten Tage nach den Öffnungsschritten bereits miteinbezogen.

Das Wichtigste in Kürze
- Der R-Wert liegt neu bei 0,98 und damit wieder unter 1,00.
- Die aktuell verfügbare Zeitspanne beinhaltet auch die ersten Tage mit offenen Terrassen.
Die von der ETH errechnete Reproduktionszahl für das Coronavirus in der Schweiz, der R-Wert, sinkt auf unter 1. Das bedeutet, dass vor 10 Tagen die Ansteckungszahlen rückläufig und nicht mehr exponentiell ansteigend waren. Da der R-Wert immer erst mit zeitlicher Verzögerung geschätzt werden kann, gibt er keine Auskunft über die jetzige Situation. Aber: Mit der heutigen Veröffentlichung sind auch die ersten beiden Tage nach den Lockerungsschritten miteinbezogen.
Terrassen-Öffnung ohne negative Folgen
Die neusten Zahlen geben damit dem Bundesrat ein Stück weit recht, der vor zwei Wochen erste Lockerungen beschloss. Dies obwohl die meisten seiner selbstauferlegten Richtwerte nicht erfüllt waren, darunter der R-Wert. Nun zeigt sich: Just am Tag der Umsetzung der Öffnungsschritte lag die Reproduktionszahl tatsächlich im grünen Bereich.
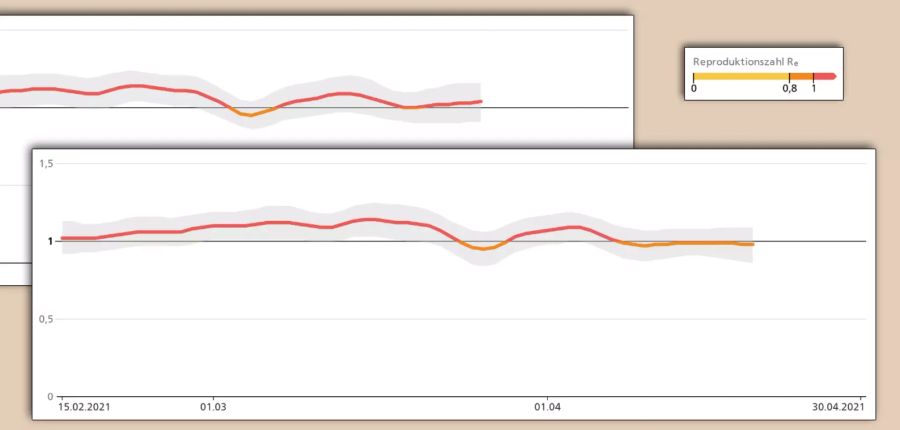
Zumindest vorläufig lässt sich also sagen: Gut gepokert. Denkbar wäre natürlich, dass ohne offene Terrassen oder Fitnesszentren der R-Wert sogar noch tiefer gelegen hätte. Jedenfalls scheinen die neu eingeflossenen Daten einiges «Gewicht» zu haben. So wurde der R-Wert auch für die Tage seit dem letzten Taucher auf unter 1 herunter korrigiert.
R-Wert des Coronavirus: Freitags genauere Schätzung
Diese nachträglichen Korrekturen des R-Werts sind gemäss ETH-Forscherin Tanja Stadler nichts Ungewöhnliches, sondern eher typisch für einen Freitag. Weil am fünften Arbeitstag die Wochenendeffekte ausgeräumt sind, können zusätzliche Daten in die Schätzung einfliessen. So werden am Freitag jeweils gleich mehrere Tage nachjustiert.

Für den Bundesrat bleibt der R-Wert weiterhin eine relevante Messgrösse, die über Lockerungen oder Verschärfungen entscheidet. Er berücksichtige dabei aber, dass der Wert eine Schätzung sei und mit statistischer Unschärfe behaftet ist.