Die wissenschaftliche Lösung für die «Zauberformel»
Gibt es einen mathematischen Ansatz für eine neue, zukunftstaugliche Zauberformel, die Sitzverteilung im Bundesrat? Ja – und er ist nicht mal kompliziert.

Das Wichtigste in Kürze
- Die Zauberformel von 1959 wird den heutigen Parteienstärken nicht mehr gerecht.
- Nau hat mit einem Mathematiker nach einer neuen Formel gesucht.
- Das Resultat ist schlank, elegant und variabel anpassbar.
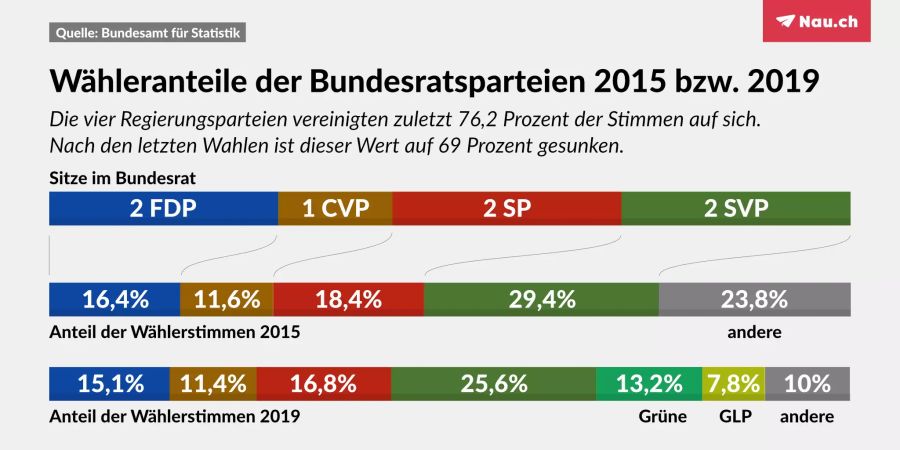
Die «Zauberformel» von 1959 war ein magischer Durchbruch – mathematisch betrachtet aber auf Primarschul-Niveau. Mit der Grünen Welle bei den letzten Wahlen taugt sie darum nicht mehr. Eine neue Formel muss her, die Rücksicht nimmt auf mehr (oder weniger) als vier Bundesratsparteien. Und trotzdem gerecht ist.
Mathematiker und die Politik
Zum Glück gibt es auch für solche Problemstellungen Experten. Zum Beispiel Philip Grech, Oberassistent am Lehrstuhl für Verhandlungsführung und Konfliktmanagement an der ETH. Er ist Mathematiker und forscht, wie und wo mathematische Modelle in der Politik angewandt werden können.
Denn eins ist klar: Auch die objektiv beste Formel muss politisch akzeptiert sein. Gerade bei gewissen politischen Forderungen hat Grech aber Vorbehalte – und nicht nur, weil sie mathematisch schwieriger abzubilden wären.
Keine Wartefrist und keine Links-Mitte-Rechts-Blöcke
Die Forderung, die Grünen müssten wie 2003 die SVP zuerst ihr gutes Resultat bestätigen, behagt Grech nicht. «Zugegeben, es gibt Kontinuitätsargumente bei einer Regierung. Warum wird aber gerade hier eine Bestätigung verlangt, aber in anderen Wahl- und Abstimmungsprozessen nicht?»
00:00 / 00:00
Das sei ja «wie wenn man jede Abstimmung zweimal im Abstand von fünf Jahren durchführen würde. Und erst wenn das Ergebnis der ersten Abstimmung bestätigt wird, mit der Umsetzung beginnen.
Auch bei der Forderung, dass dank Zauberformel keiner der Blöcke eine Mehrheit halten soll, sieht Grech Umsetzungsprobleme. Je nach Blickwinkel könnten so Sitzansprüche konstruiert werden. «Man könnte die SP zum Beispiel zu den ‹Öko-Parteien› zählen, oder die Grünliberalen zu den FDP.Liberalen oder gar den ‹Wirtschaftsparteien›.»
Schlankes Verfahren statt Zauberformel mit Spezialfällen
Wie aber erreicht man, dass die Bundesratssitze gerecht verteilt werden und ein möglichst grosses Wählersegment repräsentieren? Mindestprozentzahlen und Summenregeln könne man natürlich einführen, sagt Grech.
Das (politische) Problem: Man müsste sich auf Werte einigen, die heute plausibel, in zehn Jahren aber vielleicht unfair seien. «Es kann passieren, dass man wieder von unerwarteten Veränderungen in der Parteienlandschaft ‹überrascht› wird. Im Prinzip ist das ja auch das Problem der Zauberformel.»

«Mit der Brille des Mathematikers wäre mir ein schlankes Verfahren lieber, das nicht diverse Spezialfälle abdecken muss», sagt Grech darum. Für ein kleines Gremium wie den Bundesrat heisse das: Ein Divisorverfahren mit Standardrundung. Ein solches ist nur unwesentlich komplizierter als Primarschulstoff.
Pukelsheim lässt grüssen
Mit dem «Sainte-Laguë-Verfahren» liesse sich verhindern, dass eine grosse Partei überproportional viel Macht hat. Man sucht einen Teiler, der die Wähleranteile auf genau sieben Sitze verteilt. Im aktuellen Beispiel wäre das etwa 14,25. Das ist das gleiche Prinzip, das auch in der ersten Hälfte des «doppelten Pukelsheim» zur Anwendung gelangt.
Friedrich Pukelsheim, der dieses geniale Wahlsystem ursprünglich für den Kanton Zürich entwickelt hat, grüsst derweil freundlich aus Augsburg. Für die Zauberformel der Zukunft habe er leider keinen knackigen Vorschlag. Nur so viel: «Ich werde jedenfalls mit Interesse verfolgen, wie es bei Ihnen mit der Regierungsbildung ausgehen wird.»
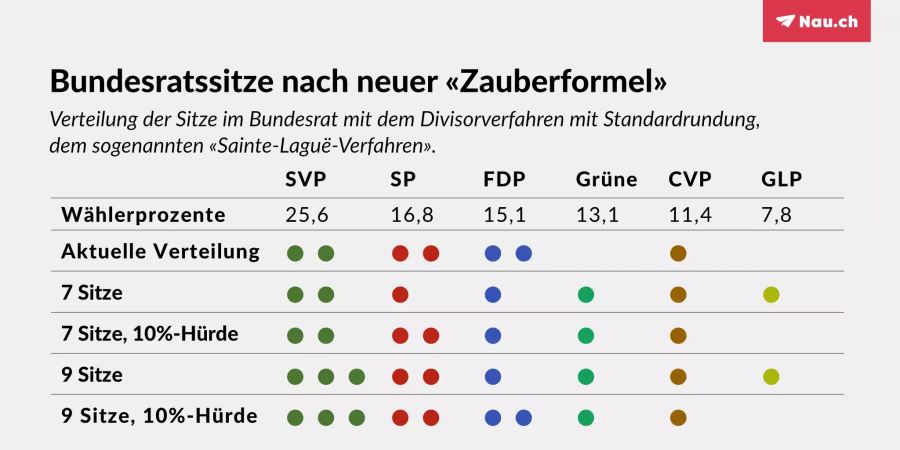
Grüne erhalten einen Sitz
Das Verfahren mit Standardrundung ist schlank und elegant. Man kann es auf sieben oder auch neun Bundesräte anwenden. Man kann die Wähleranteile oder die Anzahl Sitze im Parlament als Berechnungsgrundlage verwenden – hier darf die Politik entscheiden.
Oder man kann es mit einer Mindestprozentzahl kombinieren. «Dass man zum Beispiel nur diejenigen Parteien für die Berechnung berücksichtigt, die mindestens 10 Prozent haben», erklärt Grech. So würde verhindert, dass immer wieder kleine Parteien in die Landesregierung reinrutschen.
«Aber selbst dann muss man hoffen, dass immer mindestens eine Partei existiert, die immerhin auf 10% kommt», mahnt Grech. «Und dass es nicht irgendwann ganz viele Parteilose gibt.» Ob Formel mit Zauber oder Formel mit Logik: «Natürlich ist auch dies nicht über alle Zweifel erhaben.»









